באדיבות וויקיפדיה
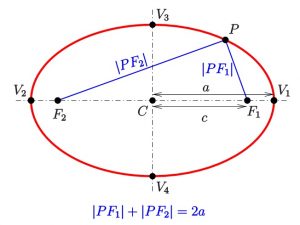
החוק הראשון של קפלר של תנועה פלנטרית אומר שכל כוכב לכת מקיף את השמש במסלול אליפטי, כאשר השמש נמצאת באחד המוקדים. מה זה אומר? אתה יכול לצייר אליפסה בדרך פשוטה זו: לקחת חתיכת חוט באורך עשרה עד חמישה עשר ס"מ ולקשור אותו בלולאה. שים שתי אצבעות על פיסת קרטון. לולאה עוברת סביב האצבעות, הכנס עיפרון ללולאה ומתח את הלולאה. עתה יש להזיז את העיפרון כאשר האבצעות יציבות על הקרטון, יש לשמור על לולאה מתוחה כאשר העיפרון נע במסלולו. התוצאה תהיה אליפסה. כל אצבע תופסת נקודה מיוחדת באליפסה הנקראת מוקד.
על פי החוק הראשון של קפלר, אם האליפסה שציירה מייצגת את מסלולו של כוכב לכת, השמש תהיה ממוקמת באחד המוקדים. אך מה מונח במוקד השני? שום דבר – זהו רק מושג מתמטי. אם מזיזים את שני המוקדים קרוב יותר, האליפסה מתקרבת למעגל. אנחנו יכולים להמשיך את ההתקדמות הזאת עד ששתי המוקדים ייפגשו באותה נקודה, אז תהפורך האליפסה למעגל מושלם. במילים אחרות, מעגל הוא רק מקרה מיוחד של אליפסה. היוונים העדיפו מסלולים מעגליים משום שמעגל הוא הצורה הפשוטה והסימטרית ביותר. עכשיו הופיעה דרך אחרת לחשיבה על מסלולים: המסלולים הם משפחה שלמה של אליפסות – שצורתן כמעגלים "מעוכים" יותר ויותר – והמעגל הוא רק מקרה פרטי של אליפסות האלה. האליפסה היא הצורה הכללית יותר. הכלליות של התיאור שבחר קפלר היא לעתים קרובות סימן ההיכר של רעיון מדעי טוב.
מעגל יכול להיות מתואר על ידי מספר אחד בלבד: הרדיוס. אבל יש צורך בשני מספרים כדי לתאר אליפסה. הקוטר הרחב ביותר של האליפסה נקרא הציר המרכזי ומחצית המרחק הזה הוא הציר המרכזי. הסימון a מייצג את מחצית הציר המרכזי, שהוא לא רק המרחק ממרכז האליפסה עד קצה אחד שלה; אלא הוא גם שווה למרחק הממוצע של כוכב לכת מהשמש. לכן הוא דומה לרדיוס של מסלול מעגלי. המילה המשמשת לתיאור מידת הפחיסות של אליפסה היא אקסצנטריות (מסומנת באות e). מבחינה מתמטית, זהו היחס בין מרחק המוקדים לבין הציר המרכזי (2a). למעגל אקסצנטריות אפס; המרחק בין המוקדים הוא אפס. רוב כוכבי הלכת נמצאים במסלולים כמעט מעגליים עם אקסצנטריות נמוכה ביותר. מסלולים פחוסים מאוד או מוארכים יש אקסצנטריות גבוהה. למרבית השביטים במסלולים אקסצנטריים מאוד, אבל הם עדיין נשמעים לחוק הראשון של קפלר: מסלולי השבטים אליפטיים, והשמש נמצאת באחד המוקדים.
באדיבות וויקיפדיה
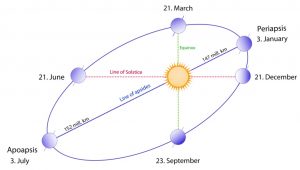
תנועה אליפטית מציעה דוגמה טובה להתקדמות המדע כאשר נאספים נתונים מדויקים יותר. אם היו בנמצא רק מדידות של תנועות כוכבי הלכת ברמד דיוק של 10% הרי מסלולים של רוב כוכבי הלכת היו מתאימים לתנועה מעגלית. אבל זיהוי של חריגה מתנועה אחידה מצריכות נתונים בדיוק המגיע ל- 1%. זיהוי החריגות הוא עניין מתוחכם, ולכן נדרשו המדידות המדוייקות של טייכו כדי לחולל את פריצת הדרך. לדוגמה, במסלול האליפטי של כדור הארץ, המרחק בין כדור הארץ לשמש משתנה רק בין 3.4% כאשר כדור הארץ נמצא בנקודה הקרובה ביותר לשמש (הנקראת "פריהליון") וכאשר הוא נמצא בנקודה הרחוקה ביותר (הנקראת "אפליון"). כלומר, במסלול האליפתי של כדור הארץ המרחק בין המוקדים הוא רק 3.4% מהציר הראשי – מעגל כמעט מושלם.
אם מודדים את המסלולים בדייקנות גבוהה יותר, ברמה של 0.1%, תגלו קיומם של פערים זעירים. במילים אחרות, למרות שכוכבי הלכת נעים במסלולים אליפטי כמעט, הם לא נעים במסלולים אליפטיים מדויקים. הסיבה לכך היא שהם חרגו מעט מתוך המסלול האלפטי שלהם בעיקבות כוח הכבידה שמפעילים עליהם כוכבי לכת אחרים. מדענים הבינו זאת כבר ב -1700. יתרה מזו, ברמה דיוק גבוהה יות, לא לגמרי נכון לטעון שהשמש ממוקמת בדיוק במוקד. במקום זאת, מוקד המסלול הוא מרכז המסה של השמש וכוכב הלכת. כדי למצוא היכן יהיה מרכז המסה, דמיינו לעצמכם מוט ארוך, ישל להניח את השמש בקצה אחד ואת הפלנטה בצד השני. מרכז המסה יהיה נקודת האיזון בין השניים. השמש כה מסיבית עד שמרכז המסה שלה עם כל פלנטה נמצא בתוך השמש, אך לא ממש במרכזה. על ידי זיהוי חריגות קלות אלה מאליפסה מושלמות בהשפעת המסלולים של כוכבי הלכת האחרים, ניתן לתאר באופן שלם יותר את תנועת הפלנטות. איסוף נתונים ברמת דיוק הולכת וגדילה עשויה להוביל להבנה חדשה לחלוטין.
Author: Chris Impey

