מסלול התנועה של פלנטה מדגים תנועה שחוזרת על עצמה באופן סדיר. כדור הארץ או כל פלנטה אחרת חולף דרך נקודה מסוימת במסלולו לאחר פרק זמן קבוע – הנקרא זמן ההקפה או זמן המחזור. מסלולי פלנטות הם רק דוגמה אחת למגוון רחב של תופעות פיזיקליות, הנקראים תהליכים מחזוריים. גלי קול או גלי ים הם דוגמאות נוספות. אנו יכולים להשתמש בחפיסת קלפים מסודרת כאנלוגיה לרצף מחזורי. תארו לעצמכם חפיסת קלפים המופרדת לערמות הקלפים בתוך ערימה מסודרים לפי סדר מספרי. הכרטיסים של כל ערך מסוים מסודרים בצורה מחזורית. לדוגמה, הג'וקרים יהיה במיקומים 13, 26, 39 ו- 52 בחפיסה. קיים מרווח אחיד, במחזור של מרווח קבוע של 13 קלפים בחפיסה של 13 קלפים. אותו מרווח קיים עבור כל ערך מספרי אחר של כרטיס. תופעות מחזוריות אחרות כגון גלים ותנודות מקיפות אותנו.
באדיבות וויקיפדיה
מסלולי הפלנטות הן תנועות חוזרות ונשנות בזמן ובמרחב: כדור הארץ עובר דרך כל נקודה מסוימת במסלולו סביב השמש בכל 365.25 ימים, והוא עוקב אחר אותו נתיב יחסית לשמש מדי שנה. כל 89 ימים מגיע מרקורי למרחק המקסימלי שלו מהשמש או להפרדה זוויתית הגדולה ביותר מן השמש. כל 75 שנים השביט של האלי חוזר מעומק החלל כדי להאיר את השמים שלנו. תנועות מחזוריות אלו וניתנות לחיזוי. תנועות הסיבוב אף היא תנועה מחזורית; כל 24 שעות השמש זורחת בגלל סיבוב כדור הארץ סביב צירו.
מסלולים הם דוגמה למגוון רחב של תופעות פיסיקליות הנקראות תהליכים מחזוריים. בואו נסתכל על כמה דוגמאות אחרות. תנודות של גוף הנע קדימה ואחורה או מצד לצד באופן קבוע. מטוטלת היא דוגמה טובה לכך – משקולת התלויה בקצה חוט עשויה להתנדנד מצד לצד. הזמן שנדרש כדי לסיים את מחזור התנועה תלוי רק באורך החוט. גלילאו גילה את העובדה המעניינת הזאת כשהיה סטודנט צעיר בפיזה. במהלך שהות בקתדרלה הוא הבחין כי מנורת מזבח מתנדנדת באותו זמן מחזור שלא תלוי במשרעת שלה. תנועה מחזורית זו של המטוטלת הפכה חלק חיוני של שעונים במשך מאות שנים.
חפצים מכאניים יכולים לרטוט באופן קבוע. אם אתם מחזיקים סרגל מעץ או מתכת, כך שהוא בולט מקצה השולחן ואז מכים בקצה הבולט, תוכלו לראות רטט או תנועה מחזורית מהירה. בדרך כלל תנועה זו מטושטשת, אבל אם הקצה הבולט של הסרגל ארוך דיו ניתן לראות כמה מחזורי תנועה מתרחשים בכל שנייה. תנודות מכניות יכולות להיות מהירות מאוד. רוב המוסיקאים מכוונים את כלי הנגינה באמצעות מזלג כוונון הרוטט 440 פעמים בשנייה! כעת אנו יכולים להמשיך ולראות את הקשר של רטט זה לתהליך מחזורי נוסף: גלים. הרטט המהיר של זרועות מזלג הכוונון יוצר שינוי מחזורי בצפיפות האוויר שאנו שומעים כגל קול. רטט של 440 פעמים בשנייה מתאים לצליל נמוך יחסית לאמצע הסולם המוסיקלי שאוזן אנושית יכולה לשמוע.
מספר תופעות מגוונות לכאורה – מסלולים, סיבובים, תנודות, תנודות וגלים – חולקים תכונות משותפות. כולם עוקבים אחר זמן המחזור; כלומר, תנועה או התנהגות שחוזרת על עצמה. הזמן שנדרש כדי להשלים מחזור הוא זמן המחזור, המסומן בדרך כלל ב- T מספר מחזורים לשנייה היא התדירות, המסומנת ב- F שתי גדלים אילו קשורים בקשר מתמטי פשוט:
f = 1 / T
יחידת התדירות של מספר המחזורים בשנייה אחת נקראת הרץ, על שמו של הפיזיקאי הגרמני היינריך הרץ. במקרה של מסלולים אנו משתמשים בגודל קרוב הקרוי מהירות זוויתית, או תדירות זוויתית, המסומנת על ידי האות היוונית אומגה ω . כל גוף משלים סיבוב בזווית של 360 מעלות או 2π רדיאנים. התדירות זוויתית היא מספר רדיאנים שעבר הגוף בשנייה:
ω= 2πf = 2π / T
באדיבות וויקפדיה
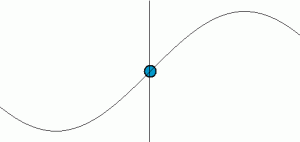
בבואנו לתאר מערכות פיזיות קטנות יותר, זמן המחזור מתקצר והתדירות עולה. גופים קטנים יותר מסתובבים (או מתנדנדים או רוטטים) מהר יותר! התנהגות זו בולטת גם במערכת השמש, שבה לפלנטות הנעות במסלולים קטנים יש זמני מחזור קצרים יותר. ניתן לראות זאת בדוגמה של סרגל הרוטט בקצה השולחן. כאשר הסרגל רוטט, ניתן להזיז את קצהו הבולט מעבר לשולחן פחות או יותר, ולראות כיצד משתנה התדר של תנועתו. התנהגות דומה מוכרת גם מעולם התנודות והצלילים. למיתרי פסנתר קצרים יש תנודות מהירות יותר מאשר למיתרים הארוכים, והם יוצרים לצלילים גבוהים יותר. כמו כן, ניתן ליצור צלילים בתדירות הגבוהה ביותר בכלי הנשיפה הקטן ביותר. נסו לחשוב על חצוצרה לעומת טובה או פיקולו לעומת בסון. קיים דמיון בולט נוסף בין התהליכים מחזוריים שונים. התנועות שלהם בממד אחד מתוארות על ידי פונקציה סינוסואידלית. תנועה או תזוזה מן המרכז ניתנת על ידי הביטוי:
X = Xmaxcos (ωt) = Xmaxcos (2πft)
הסטייה המרבית מהמרכז מיוצגת על-ידי ההעתק המקסימלי Xmax. המיקומים החיוביים והשליליים מתייחסים פשוט לתנועה שמאלה או ימינה מנקודת המנוחה או מהעמדה המרכזית, כך שהסטייה הכוללת היא 2Xmax. במקרה של מסלול כדור הארץ סביב השמש, X מייצג את ההפרדה הנראית לעין בין כדור הארץ לשמש, כאשר מתבוננים במסלול ממישור המלקה. במקרה של סיבוב כדור הארץ, X הוא המרחק הנראה לעין בין כל נקודה על פני השטח לבין ציר הסיבוב, כאשר מתבוננים בסיבוב ממישור קו המשווה. בכל יתר הדוגמאות, X הוא ההעתק של הגוף מנקודת המנוחה או מהמיקום המרכזי שלו. בגלי קול, X מייצג את השינוי בצפיפות האוויר כאשר הגל עובר דרך נקודה מסוימת. ראוי לציין כי מגוון רחב כל כך של תופעות ניתן לתיאור באמצעות אותה משוואה פשוטה.

