מעט מאוד מדענים יוצרים תיאוריות חדשות או מגלים חוקי טבע. העבודה של מדען מתבססת על איסוף נתונים וגיבוש הידע הקיים. השערה היא הסבר מוצע לקבוצת מדידות שבוצעו בחלל או במעבדה. הניסוח המתמטי של ההשערה נקרא מודל. מדענים בודקים השערות על ידי איסוף נתונים בהיקף גדול ודיוק גבוה.
לפניכם דוגמה חשובה של בדיקת ההשערה מן ההיסטוריה של האסטרונומיה. ההשערה הקופרניקאית הייתה שהפלנטות סובבות סביב השמש במסלולים מעגליים. לפי השערה זו המהירות המסלולית של הפלנטה הייתה זהה בכל נקודה במסלול מעגלי. לכן, המהירות של מאדים למשל, לא צריכה להשתנות. (המדידה בפועל היא של מהירות זוויתית על רקע השמים, כאשר ניתן להמיר את מהירות הזוויתית למהירות בחלל אם יודעים את המרחק למאדים). סיבוך נוסף במדידת המהירות נובע מן העובדה כי המדידה נעשית לא מהשמש אלא מן כדור הארץ, שהוא עצמו נע בחלל.
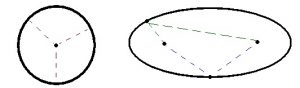
קפלר ידע שהמהירות הזוויתית של מאדים לא הייתה קבועה והוא הניח שהמסלול הוא אליפטי. אנו יכולים להשתמש בחוקי קפלר כדי לחשב מה המשמעות של מסלול אליפטי לגבי מהירות המאדים. למאדים יש אקסצנטריות מסלולית של 0.093. אם r מייצג את המרחק הממוצע מהשמש, מסלול מאדים נמצא בין r1.093 לבין r0.907. במסלולים אליפטיים מהירות הפלנטה משתנה ביחס למרחק מהשמש בהתאם לביטוי:
ν ∝ √ r
לכן, מהירות מאדים משתנה בצורה חלקה בין:
√ 1.093 ν = 1.045 ν
לבין:
√0.907 ν = 0.952 ν
במילים אחרות, המהירות המסלולית של מאדים נעה בין 4.5% מעל הממוצע ל -4.76% מתחת לממוצע לערך; כך שנדרש שינוי של 9% לערך במהירות מאדים כדי שניתן יהיה לזהות את התנועה האליפטית – ולשלול את ההשערה של מסלול מעגלי. לשם כך דורשה מדידה ברמת דיוק של 9% לפחות. ניתן לשפר את הבדיקה של השערה זו בעזרת מדידות נוספות, או בסיוע מדידות מדויקות יותר, או בעזרת שתי השיטות.
נעבור עתה לבדיקת דוגמה מעוררת עניין המעסיקה כיום רבים מקהילת האסטרונומים – זיהוי של פלנטות מחוץ למערכת השמש. תנודות של כוכב מספקת הזדמנות לזהות פלנטה בלתי נראית בשל השפעת כוח הכבידה שלה על הכוכב. נניח שאנו צופים במדויק את מהירותו של כוכב, הדומה לשמש שלנו, ומחפשים את השינויים במהירות של הכוכב כתוצאה מתנועת פלטנה המקיפה אותו. אם הנתונים מראים קיומם של שינויים ברורים בתנועת הכוכב אנו יכולים לחשב את המסה של הפלנטה, המסוגלת לגרום לשינויים אלה. במקרה זה, אסטרונומים יכולים לאשר את ההשערה שפלנטה מקיפה את הכוכב ולמדוד את מסתה של הפלנטה שמסתה כמסת צדק.
המחקר העוסק בגילוי פלנטות מחוץ למערכת השמש יכול לשמש כדוגמה לבדיקת השערה בדיוק רב ביותר. ייתכן שהנתונים לא יהיו מדויקים דיים כדי לבחון את ההשערה של פלנטה שמסתה כמסת צדק. לא ניתן לבחון השערה כאשר האפקט שאנו מחפשים קטן מאוד. השינויים בתנודות הכוכב בהשפעת פלנטה שמסתה כמסת כדור הארץ היא רק m/s 0.09. השפעה זו הנמדדת בעזרת אפקט דופלר, תגרום למדידת שינויים הקטנים פי 100 מהשינויים שתצור פלנטה שמסתה כמסת צדק. ניתן לדמיין את כמות הנתונים מדויקים הנדרשת כדי לבחון ההשערה בדבר קיומה של פלנטה שמסתה כמסת כדור הארץ. לפעמים אסטרונומים סובלים ממחסור בנתונים. תצפיות המשתרעות על פני מרווח של 5 שנים אינן מספיקות כדי לתאר מחזור שלם של תנודות בעקומת האור. כך שאפילו ההשערה בדבר קיומה של פלנטה שמסתה כמסת צדק אינה ניתנת לבדיקה.
באדיבות NASA
המצב יכול להיות אפילו גרוע יותר אם היינו מחפשים פלנטה רחוקה עוד יותר מהכוכב שלה. אורנוס מקיף את השמש ב- 84 שנים, כך שנדרשות כמעט מאה שנים כדי לאסוף נותנים במטרה לזהות קיומה של פלנטה בעלת זמן מחזור שכזה. לבסוף יתכן כי נתונים מדויקים אינם מראים שינויים משמעותיים ממהירות קבועה. הנתונים מצביעים על שינויים קטנים יותר מאשר התחזית עבור פלנטה שמסתה כמסת צדק. נתונים אלה מאפשרים לנו לדחות את ההשערה בדבר קיומה של פלנטה שמסתה כמסת צדק. בבדיקת ההשערה יש לבחון שלושה משתנים: מספר התצפיות, השגיאה בכל תצפית, והחריגה של התצפית מהתחזית של השערה או מודל. מבחינה מתמטית, ניתן לכתוב:
c2 = Σ [(xdata – xmodel)2 / σ (x)2]
במשוואה זו יש לקחת את הריבוע של ההפרש בין הנתונים לבין המודל בכל נקודה, לחלק אותו בריבוע של שגיאה בתצפית – σ, ולסכם את הכמות על פני כל נקודות הנתונים. (סכום הכמויות מיוצג במתמטיקה על ידי האות יוונית סיגמא, Σ.) למעשה, זהו חישוב של הסכום שבו הנתונים חורגים מן המודל. הכמות x יכולה להיות כל כמות ניתנת למדידה: עוצמת האור, מהירות, עוצמת השדה המגנטי וכן הלאה. במודל טוב קיימת סטייה מועטה של הנתונים כך של- c2 יש ערך נמוך. מודל גרוע מיוצג על ידי סטייה גדולה של הנתונים מערכי המודל, של- c2 יש ערך גבוה. שיטה זו לבדיקת מודל או השערה נמצאת בלב המחקר המדעי.

